GE : 1x2x2 intermediate good
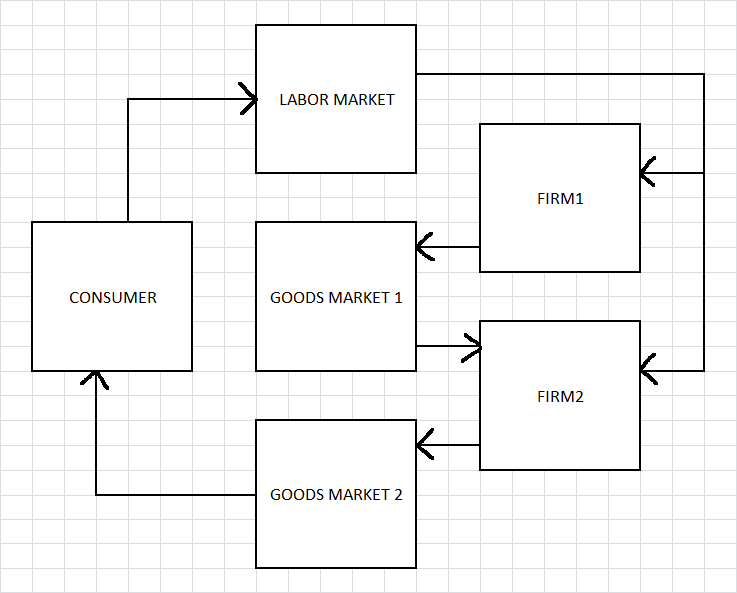
| LABOR MARKET, w[0] | |
| SUPPLY | DEMAND |
CONSUMER : n^* | FIRM1 : z_0^* FIRM2 : z_1^* |
| MIDDLE MARKET, p[0] | |
| SUPPLY | DEMAND |
FIRM1 : y_0^* | FIRM2 : k_1^* |
| GOODS MARKET, p[1] | |
| SUPPLY | DEMAND |
FIRM2 : y_1^* | CONSUMER : x^* |

| LABOR MARKET, w[0] | |
| SUPPLY | DEMAND |
CONSUMER : n^* | FIRM1 : z_0^* FIRM2 : z_1^* |
| MIDDLE MARKET, p[0] | |
| SUPPLY | DEMAND |
FIRM1 : y_0^* | FIRM2 : k_1^* |
| GOODS MARKET, p[1] | |
| SUPPLY | DEMAND |
FIRM2 : y_1^* | CONSUMER : x^* |
FIRM[0] | FIRM[1] | CONSUMER |
|
\pi_0 = p_0 \cdot z_0^{\alpha} - w z_0 z_0^* = \bigg ( \dfrac{w}{p_0 \alpha} \bigg ) ^ {\frac{1}{\alpha-1}} y_0^* = \bigg ( \dfrac{w}{p_0 \alpha} \bigg ) ^ {\frac{\alpha}{\alpha-1}} \pi_0 = p_0 \cdot \bigg ( \dfrac{w}{p_0 \alpha} \bigg ) ^ {\frac{\alpha}{\alpha-1}} - w \bigg ( \dfrac{w}{p_0 \alpha} \bigg ) ^ {\frac{1}{\alpha-1}} |
\pi_1 = p_1 \cdot z_1^{\beta}(k_1+1)^{1-\beta} - w z_1 - p_0 k_1 From the FOCs, the expansion path : \dfrac{\beta}{1-\beta} \cdot \dfrac{k_1+1}{z_1} = \dfrac{w}{p_0} z_1^{expansion} = \dfrac{\beta}{1-\beta} \cdot \dfrac{p_0}{w} \cdot (k_1 + 1) FIRM[1] production is pretty much CRS. If it could, it would keep buying z_1 and k_1 forever. So it only follows the expansion path until it runs out of one of them.
I am assuming it will run out of k_1 first. But k_1 is limited by how much y_0 there is. z_1^* = \bigg ( \dfrac{w}{p_1 \beta} \bigg ) ^ {\frac{1}{\beta-1}} (\bar{k_1}+1) k_1^*=y_0^* |
u = \ln x + \gamma \ln b M = wL + \theta_0 + \theta_1
|
u = \ln [n_2^{\beta}(n_1^{\alpha}+1)^{1-\beta}] + \gamma \ln (L-n_1-n_2)
u = \beta \ln n_2 + (1-\beta) \ln (n_1^{\alpha}+1) + \gamma \ln (L-n_1-n_2)
(3) : from du/dn2 n_2 = \frac{\beta}{\gamma+\beta} \cdot (L-n_1)
(4) : from du/dn1 n_2 = -A n_1^{1-\alpha} - (A+1)n_1 + L where A= \dfrac{\gamma}{\alpha(1-\beta)}
Solution : 0 = -A n_1^{1-\alpha} - (A-B+1) n_1 + (1-B)L where B = \frac{\beta}{\gamma+\beta}
idk how to solve this except for numerically.
So the solution to this problem seems to be (from here):
p_1y_1 - y_1(wR^{\beta-1} + p_0R^{\beta}) + p_0, where R=\dfrac{(1-\beta)w}{\beta p_0}
But it means firm1 commits to following the expansion path
sub the expansion-ratios into the production function to get z=f(y) and k=f(y)
and if we follow that thru to the profit function, we can solve for p1 in terms of p0, and it get us to an allocation that coincides with the central planner's allocation.
but that is mysterious to me. as opposed to a firm taking a price as given, and making a choice to hire along the expansion path, then when they run out of one good, resorting to a single variable max problem. that seems to make more sense in the spirit of the firm taking the price as given.
and what about all the other vectors that work? (the orange line)
the weird thing about it is that, when we solve like above, we're basically saying, what MUST the price be, in order to PERMIT FIRM1 to expand along its ideal expansion path.
does that make the allocation legit?
because the whole system CAN work with other prices, with FIRM1 making concessions, eating up all the K and then doing the max problem based on Z alone.
| PARAMETERS | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
alpha | makes firm[0] more important | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
beta | makes firm[0] less important | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
gamma | how lazy you are | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L | time endowment | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CENTRALLY PLANNED | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n_0 = 0 | n_0 \ge 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n0 | 0 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n1 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| k | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| u | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| p0 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| p1 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||